Automatic Tuning for Factor Graph-Based Estimation Using Bayesian Optimisation
In robotics, state estimation systems such as Simultaneous Localisation and Mapping (SLAM) often rely on manually tuned noise parameters — a process that is time-consuming, subjective, and error-prone. While previous work has automated tuning for Kalman Filters, this dissertation extended those ideas to the more flexible and complex world of factor graphs.
The goal was to create a proof-of-concept system that could automatically tune a factor graph’s process and measurement noise parameters using Bayesian Optimisation (BO). To measure estimator quality, the project adapted two statistical consistency metrics:
- Consistent Normalised Estimation Error Squared (CNEES) — checks whether the true estimation error matches the predicted uncertainty.
- Consistent Normalised Innovation Squared (CNIS) — tests whether measurement residuals are unbiased and uncorrelated (“white”).
These metrics formed the backbone of the automatic tuning framework.
⚙️ How It Worked — The Method
The project was built around a 2D tracking simulation designed to test and validate the tuning pipeline.
- System Design: Implemented both a linear (Constant Velocity) and non-linear (Constant Turn) motion model to estimate true process noise (V) and measurement noise (σ²).
- Exploring the Problem: Conducted an exhaustive grid search across parameter space to visualise the CNIS cost surface. This revealed a broad, flat diagonal valley where many parameter combinations produced similar consistency — a key reason manual tuning feels ambiguous.
- Proposed Solution: Introduced Bayesian Optimisation to search the parameter space efficiently. BO used a Gaussian Process model to predict promising regions, cutting computation dramatically compared to brute-force search.
- Monte Carlo Stability: Early experiments with small Monte Carlo samples ((N = 500)) led to unstable CNIS results. Stability was achieved only after increasing runs to (N = 5000 to 10000), ensuring a smooth cost surface for the optimiser to follow.
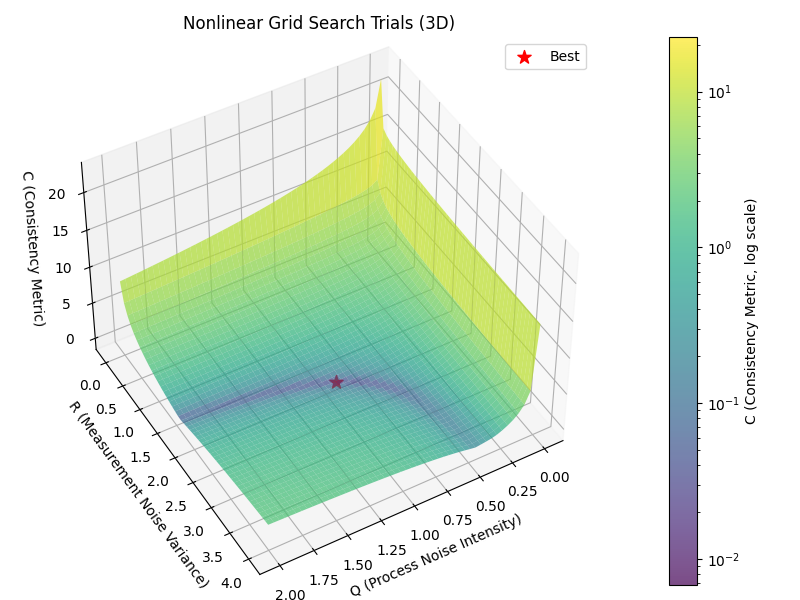
📊 What I Found — Results & The Twist
Bayesian Optimisation worked exactly as intended — it quickly converged to the optimal region within the CNIS cost valley. However, the most interesting result came from comparing statistical consistency (CNIS) against tracking accuracy (Mean Squared Error, MSE):
- There was almost zero correlation between CNIS and MSE.
- The factor-graph estimator proved highly robust: both the “true” parameters and the BO-tuned ones produced similarly low tracking errors.
- Within the cost valley, any “good enough” parameter set gave near-identical performance.
This revealed a fundamental insight — tuning purely for statistical consistency doesn’t necessarily improve real-world performance. Due to the robustness of the Factor Graph, a simple guess of these noise paramters is sufficient, as long as you are close enough.
🧭 Conclusion & Future Work
The dissertation successfully demonstrated an automated tuning framework for factor-graph-based estimation, validating the use of Bayesian Optimisation to replace manual noise tuning.
Future work could extend this approach to multi-objective optimisation, balancing statistical soundness with practical accuracy, or integrate parallelised optimisation for large-scale SLAM applications.
I am currently working on Publishing this paper and will attach a Link when I have completed the process. In the meantime check out the GitHub Repo for a better understanding of the project as well as the full length paper below